算法题

两数之和

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> map = new HashMap<>();
        for(int i = 0;i < nums.length; i++) {
            if(map.containsKey(target - nums[i])){
                return new int[]{map.get(target - nums[i]), i};
            }
            map.put(nums[i], i);
        }
        return null;
    }
}

二分查找法

public static int binarySearch(int[] a, int target) {
    int i = 0, j = a.length - 1;
    while (i <= j) {
        int m = (i + j) >> 1;
        if (target < a[m]) {
            j = m - 1;
        } else if (target > a[m]) {
            i = m + 1;
        } else {
            return m;
        }

    }
    return -1;
}

public static int binarySearch(int[] a, int target) {
    int i = 0, j = a.length;
    while (i < j) {
        int m = (i + j) >> 1;
        if (target < a[m]) {
            j = m;
        } else if (target > a[m]) {
            i = m + 1;
        } else {
            return m;
        }

    }
    return -1;
}

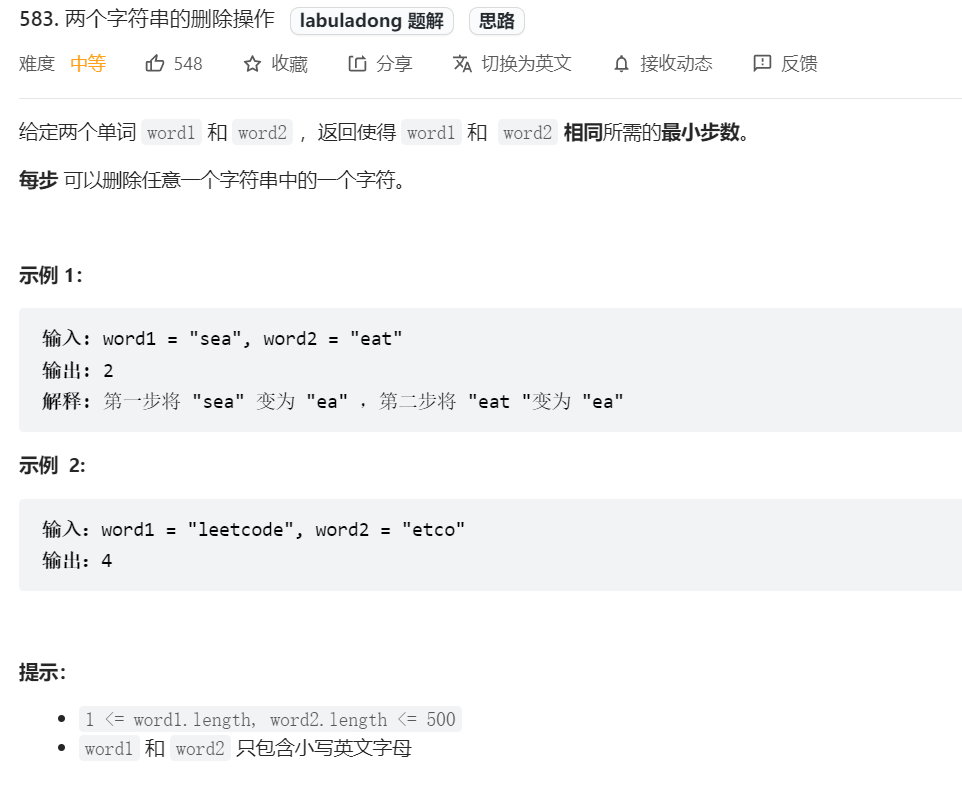
class Solution {
    public int minDistance(String s1, String s2) {
        int m = s1.length(), n = s2.length();
        int lcs = longestCommonSubsequence(s1, s2);
        //删去相同的字母，剩下的就是最小步数。
        return m - lcs + n - lcs;
    }

    int longestCommonSubsequence(String s1, String s2){
        int m = s1.length(), n = s2.length();
        int[][] dp = new int[m + 1][n + 1];

        for(int i = 1;i <= m;i++){
            for(int j = 1;j <= n;j++){
                if(s1.charAt(i - 1) == s2.charAt(j - 1)){
                    dp[i][j] = dp[i-1][j-1] + 1;
                }else {
                    dp[i][j] = Math.max(dp[i][j-1], dp[i-1][j]);
                }
            }
        }
        return dp[m][n];
    }
}

快速排序

public class QKSort {
    int n;

    public static void quick_sort(int q[], int l, int r) {
        if (l >= r) return;
        int x = q[l], i = l - 1, j = r + 1;
        while (i < j){
            do i++;while (q[i] < x);
            do j--;while (q[j] > x);
            if (i < j) {
                int temp = q[i];
                q[i] = q[j];
                q[j] = temp;
            }
        }

        quick_sort(q, l, j);
        quick_sort(q, j + 1, r);
    }


    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        float v = (float) (1e6 + 10);
        int q[] = new int[(int) v];
        int n = scanner.nextInt();
        for (int i = 0; i < n; i++) {
            q[i] = scanner.nextInt();
        }
        quick_sort(q, 0, n - 1);
        for (int i = 0; i < n; i++) {
            System.out.print(q[i] + " ");
        }
    }
}

归并排序

public class MergeSort {
    static int v = 1000010;
    static int[] q = new int[v];
    static int[] tmp = new int[v];
    public static void merge_sort(int q[], int l, int r){
        if(l >= r) return;

        int mid = r + l >> 1;
        merge_sort(q, l, mid);
        merge_sort(q, mid + 1, r);

        int k = 0, i = l,j = mid + 1;
        while (i < mid && j <= r)
            if(q[i] <= q[j]) tmp[k++] = q[i++];
            else tmp[k++] = q[j++];
        while (i <= mid) tmp[k++] = q[i++];
        while (j <= r) tmp[k++] = q[j++];

        for (i = l,j = 0;i <= r;i++)
            q[i] = tmp[j];
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        Integer n = scanner.nextInt();
        for (int i = 0; i < n; i++) {
            scanner.nextInt();
        }
        merge_sort(q, 0, n - 1);

        for (int i = 0; i < n; i++) {
            System.out.print(q[i] + " ");
        }
    }
}

旋转数组

使用临时数组

	public void rotate(int nums[], int k) {
        int length = nums.length;
        int temp[] = new int[length];
        //把原数组值放到一个临时数组中，
        for (int i = 0; i < length; i++) {
            temp[i] = nums[i];
        }
        //然后在把临时数组的值重新放到原数组，并且往右移动k位
        for (int i = 0; i < length; i++) {
            nums[(i + k) % length] = temp[i];
        }
    }

多次反转

public void rotate(int[] nums, int k) {
       int length = nums.length;
       k %= length;
       reverse(nums, 0, length - 1);//先反转全部的元素
       reverse(nums, 0, k - 1);//在反转前k个元素
       reverse(nums, k, length - 1);//接着反转剩余的
   }

   //把数组中从[start，end]之间的元素两两交换,也就是反转
   public void reverse(int[] nums, int start, int end) {
       while (start < end) {
           int temp = nums[start];
           nums[start++] = nums[end];
           nums[end--] = temp;
       }
   }

public void rotate(int[] nums, int k) {
      int length = nums.length;
      k %= length;
      reverse(nums, 0, length - k - 1);//先反转前面的
      reverse(nums, length - k, length - 1);//接着反转后面k个
      reverse(nums, 0, length - 1);//最后在反转全部的元素
  }

  //把数组中从[start，end]之间的元素两两交换,也就是反转
  public void reverse(int[] nums, int start, int end) {
      while (start < end) {
          int temp = nums[start];
          nums[start++] = nums[end];
          nums[end--] = temp;
      }
  }

环形旋转
    public static void rotate(int[] nums, int k) {
        int hold = nums[0];
        int index = 0;
        int length = nums.length;
        boolean[] visited = new boolean[length];
        for (int i = 0; i < length; i++) {
            index = (index + k) % length;
            if (visited[index]) {
                //如果访问过，再次访问的话，会出现原地打转的现象，
                //不能再访问当前元素了，我们直接从他的下一个元素开始
                index = (index + 1) % length;
                hold = nums[index];
                i--;
            } else {
                //把当前值保存在下一个位置，保存之前要把下一个位置的
                //值给记录下来
                visited[index] = true;
                int temp = nums[index];
                nums[index] = hold;
                hold = temp;
            }
        }
    }
使用一个数组visited表示这个元素有没有被访问过，如果被访问过就从他的下一个开始，防止原地打转。

滑动窗口框架

/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
    Map<Character,Integer> need = new HashMap<>();
    Map<Character,Integer> window = new HashMap<>();
    for (char c : t.toCharArray()) 
        need.put(c, need.getOrDefault(c, 0)+1);
    
    int left = 0, right = 0;
    int count = 0; 
    while (right < s.length()) {
        // c 是将移入窗口的字符
        char c = s.charAt(right);
        // 右移窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...
 
        
        // 判断左侧窗口是否要收缩
        while (window needs shrink) {
            // d 是将移出窗口的字符
            char d = s.charAt(left);
            // 左移窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

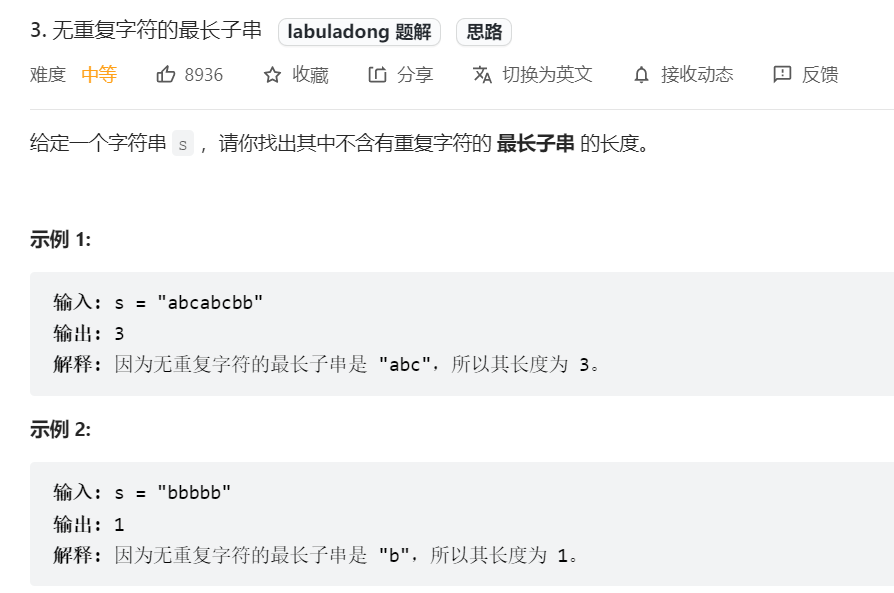
class Solution {
    public int lengthOfLongestSubstring(String s) {
        Map<Character, Integer> window = new HashMap<>();
        int left = 0, right = 0;
        int res = 0;
        while(right < s.length()){
            char c = s.charAt(right);
            right++;
            window.put(c, window.getOrDefault(c, 0) + 1);
            while(window.get(c) > 1){
                char d = s.charAt(left);
                left++;
                window.put(d, window.get(d) - 1);
            }
            res = Math.max(res, right - left);
        }
        return res;
    }
}

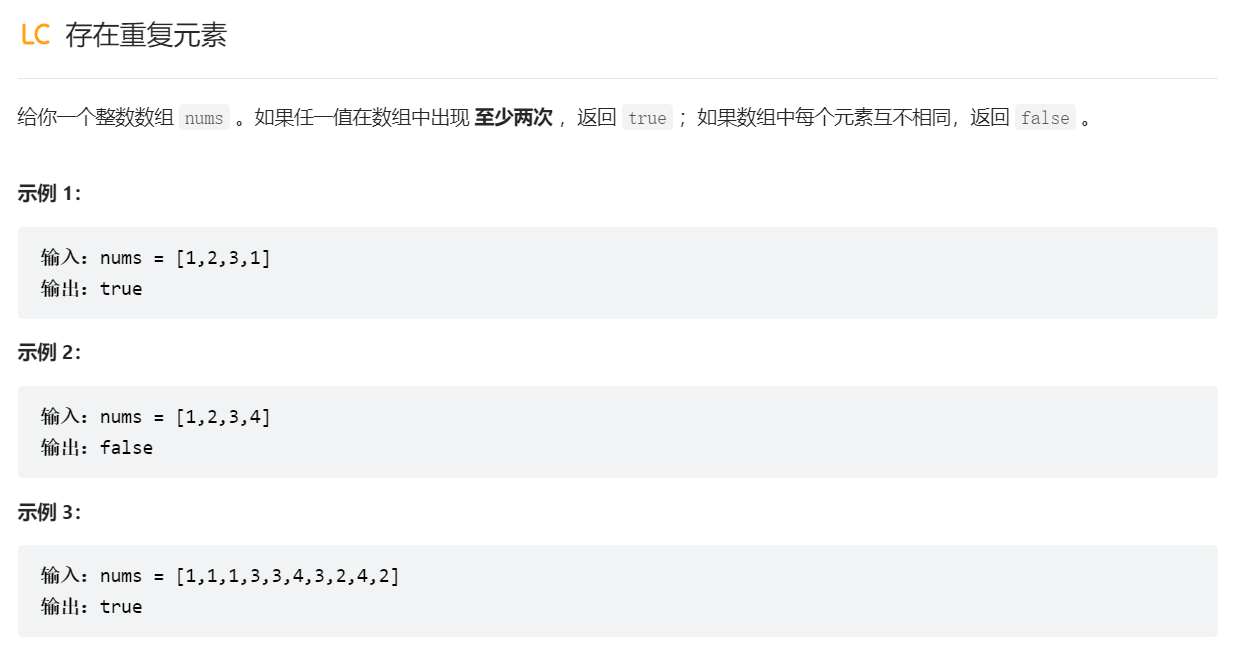
存在重复的元素

class Solution {
    public boolean containsDuplicate(int[] nums) {
        Set<Integer> set = new HashSet<>();
        for(int num : nums){
            if(!set.add(num)) return true;
        }
        return false;
    }
}

只出现一次的数字

class Solution {
    public int singleNumber(int[] nums) {
        int result = 0;
        for(int i = 0;i < nums.length;i++){
            result ^= nums[i];
        }
        return result;
    }
}

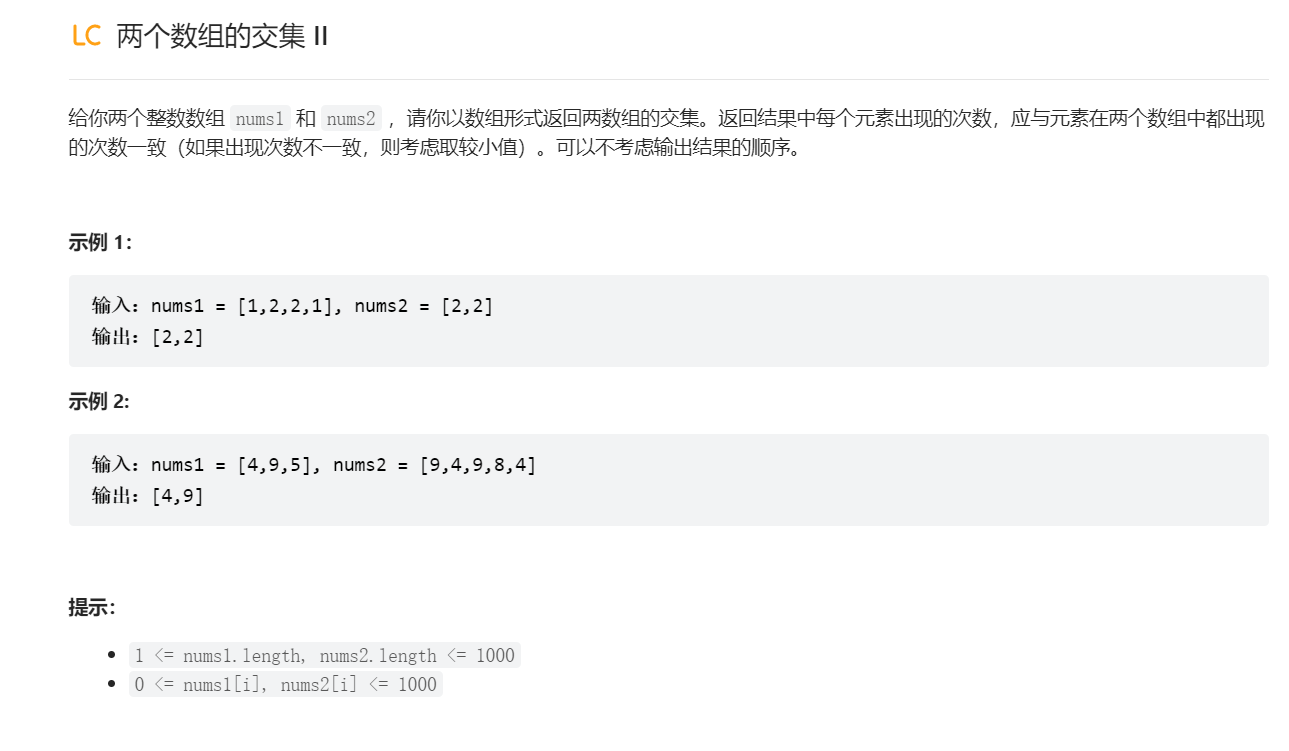
两个数组的交集

public int[] intersect(int[] nums1, int[] nums2) {
       // 先对两个数组进行排序
       Arrays.sort(nums1);
       Arrays.sort(nums2);
       int i = 0;
       int j = 0;
       List<Integer> list = new ArrayList<>();
       while (i < nums1.length && j < nums2.length) {
           if (nums1[i] < nums2[j]) {
               // 如果i指向的值小于j指向的值，，说明i指向
               // 的值小了，i往后移一步
               i++;
           } else if (nums1[i] > nums2[j]) {
               // 如果i指向的值大于j指向的值，说明j指向的值
               // 小了，j往后移一步
               j++;
           } else {
               // 如果i和j指向的值相同，说明这两个值是重复的，
               // 把他加入到集合list中，然后i和j同时都往后移一步
               list.add(nums1[i]);
               i++;
               j++;
           }
       }
       //把list转化为数组
       int index = 0;
       int[] res = new int[list.size()];
       for (int k = 0; k < list.size(); k++) {
           res[index++] = list.get(k);
       }
       return res;
   }

public int[] intersect(int[] nums1, int[] nums2) {
    HashMap<Integer, Integer> map = new HashMap<>();
    ArrayList<Integer> list = new ArrayList<>();

    //先把数组nums1的所有元素都存放到map中，其中key是数组中
    //的元素，value是这个元素出现在数组中的次数
    for (int i = 0; i < nums1.length; i++) {
        map.put(nums1[i], map.getOrDefault(nums1[i], 0) + 1);
    }

    //然后再遍历nums2数组，查看map中是否包含nums2的元素，如果包含，
    //就把当前值加入到集合list中，然后再把对应的value值减1。
    for (int i = 0; i < nums2.length; i++) {
        if (map.getOrDefault(nums2[i], 0) > 0) {
            list.add(nums2[i]);
            map.put(nums2[i], map.get(nums2[i]) - 1);
        }
    }

    //把集合list转化为数组
    int[] res = new int[list.size()];
    for (int i = 0; i < list.size(); i++) {
        res[i] = list.get(i);
    }
    return res;
}

加一

class Solution {
        public int[] plusOne(int[] digits) {
        int length = digits.length;
        for (int i = length - 1; i >= 0; i--) {
            if (digits[i] != 9) {
                //如果数组当前元素不等于9，直接加1
                //然后直接返回
                digits[i]++;
                return digits;
            } else {
                //如果数组当前元素等于9，那么加1之后
                //肯定会变为0，我们先让他变为0
                digits[i] = 0;
            }
        }
        //除非数组中的元素都是9，否则不会走到这一步，
        //如果数组的元素都是9，我们只需要把数组的长度
        //增加1，并且把数组的第一个元素置为1即可
        int temp[] = new int[length + 1];
        temp[0] = 1;
        return temp;
    }
}

移动零

public void moveZeroes(int[] nums) {
    if (nums == null || nums.length == 0)
        return;
    int index = 0;
    //一次遍历，把非零的都往前挪
    for (int i = 0; i < nums.length; i++) {
        if (nums[i] != 0)
            nums[index++] = nums[i];
    }
    //后面的都是0,
    while (index < nums.length) {
        nums[index++] = 0;
    }
}

class Solution {
    public void moveZeroes(int[] nums) {
        int i = 0;
        for(int j =0;j < nums.length;j++){
            if(nums[j] == 0) i++;
            else if(i != 0){
                nums[j -i] = nums[j];
                nums[j] = 0;
            }
        }
    }
}

class Solution {
    public void moveZeroes(int[] nums) {
        int i = 0;
        for(int j = 0;j < nums.length;j++){
            if(nums[j] != 0){
                int temp = nums[j];
                nums[j] = nums[i];
                nums[i] = temp;
                i++;
            }
        }
    }
}

有效的数独

class Solution {
    public boolean isValidSudoku(char[][] board) {
        for(int i = 0;i < 9;i++){
            boolean[] used = new boolean[10];
            for(int j = 0;j < 9;j++){
                if (board[i][j] == '.') {
                    continue;
                }
                int num = board[i][j] - '0';
                if(used[num]) {
                    return false;
                }
                used[num] = true;
            }
        }

        for(int j = 0;j < 9;j++){
            boolean[] used = new boolean[10];
            for(int i = 0;i < 9;i++){
                if(board[i][j] == '.') {
                    continue;
                }
                int num = board[i][j] - '0';
                if(used[num]) {
                    return false;
                }
                used[num] = true;
            }
        }

        for(int i = 0;i < 3;i++){
            for(int j = 0;j < 3;j++){
                boolean[] used = new boolean[10];
                for(int r = i*3;r < i * 3 + 3;r++){
                    for(int c = j * 3;c < j * 3 + 3;c ++){
                        if(board[r][c] == '.') {
                            continue;
                        }
                        int num = board[r][c] - '0';
                        if(used[num]) {
                            return false;
                        }
                        used[num] = true;
                    }
                }
            }
        }

        return true;
    }
}

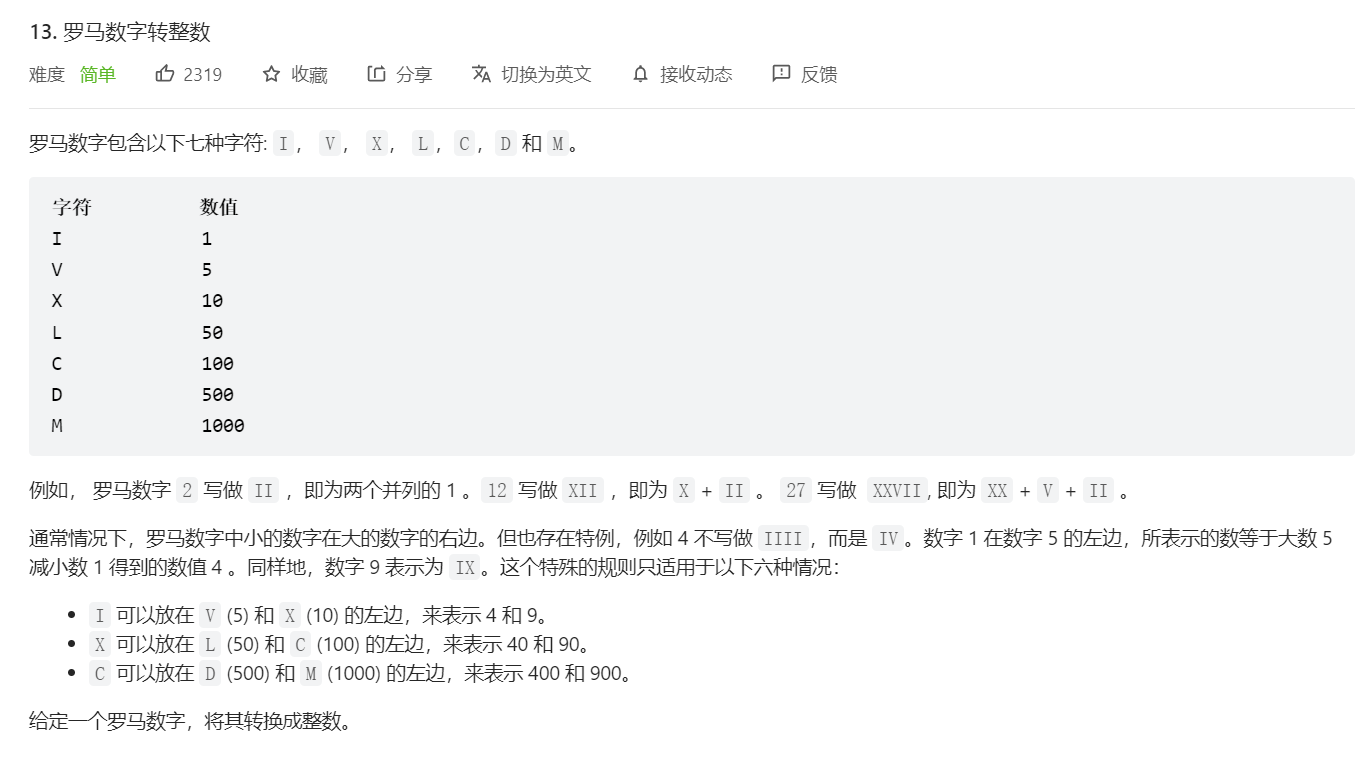
罗马数字转整数

class Solution {
    public int romanToInt(String s) {
        int num = 0;
        int perv = 0;
        for(int i = 0; i< s.length();i++){
            int curr = 0;
            switch(s.charAt(i)){
                case 'I':curr = 1;break;
                case 'V':curr = 5;break;
                case 'X':curr = 10;break;
                case 'L':curr = 50;break;
                case 'C':curr = 100;break;
                case 'D':curr = 500;break;
                case 'M':curr = 1000;break;
            }
            if(curr > perv){
                num+=curr - perv * 2;
            }else{
                num += curr;
            }
            perv = curr;
        }
        return num;
    }
}

有效的字母异位词

public boolean isAnagram(String s, String t) {
       if (s.length() != t.length())
           return false;
       int[] letterCount = new int[26];
       //统计字符串s中的每个字符的数量
       for (int i = 0; i < s.length(); i++)
           letterCount[s.charAt(i) - 'a']++;
       //减去字符串t中的每个字符的数量
       for (int i = 0; i < t.length(); i++)
           letterCount[t.charAt(i) - 'a']--;
       //如果数组letterCount的每个值都是0，返回true，否则返回false
       for (int count : letterCount)
           if (count != 0)
               return false;
       return true;
   }

优化：

public boolean isAnagram(String s, String t) {
       if (s.length() != t.length())
           return false;
       int[] letterCount = new int[26];
       //统计字符串s中的每个字符的数量
       for (int i = 0; i < s.length(); i++)
           letterCount[s.charAt(i) - 'a']++;
       //减去字符串t中的每个字符的数量
       for (int i = 0; i < t.length(); i++) {
           //如果当前字符等于0，直接返回false，
           if (letterCount[t.charAt(i) - 'a'] == 0)
               return false;
           letterCount[t.charAt(i) - 'a']--;
       }
       return true;
   }

先排序，在比较：

public boolean isAnagram(String s, String t) {
    char[] sChar = s.toCharArray();
    char[] tChar = t.toCharArray();
    //对两个字符串中的字符进行排序
    Arrays.sort(sChar);
    Arrays.sort(tChar);
    return Arrays.equals(sChar, tChar);
}

一次遍历：

public boolean isAnagram(String s, String t) {
    if (s.length() != t.length())
        return false;
    char[] cs = s.toCharArray();
    char[] ct = t.toCharArray();
    int[] map = new int[26];
    int count = 0;
    for (int i = 0; i < cs.length; i++) {
        //出现了一个新的字符
        if (++map[cs[i] - 'a'] == 1) {
            count++;
        }
        //消失了一个新的字符
        if (--map[ct[i] - 'a'] == 0) {
            count--;
        }
    }
    return count == 0;
}

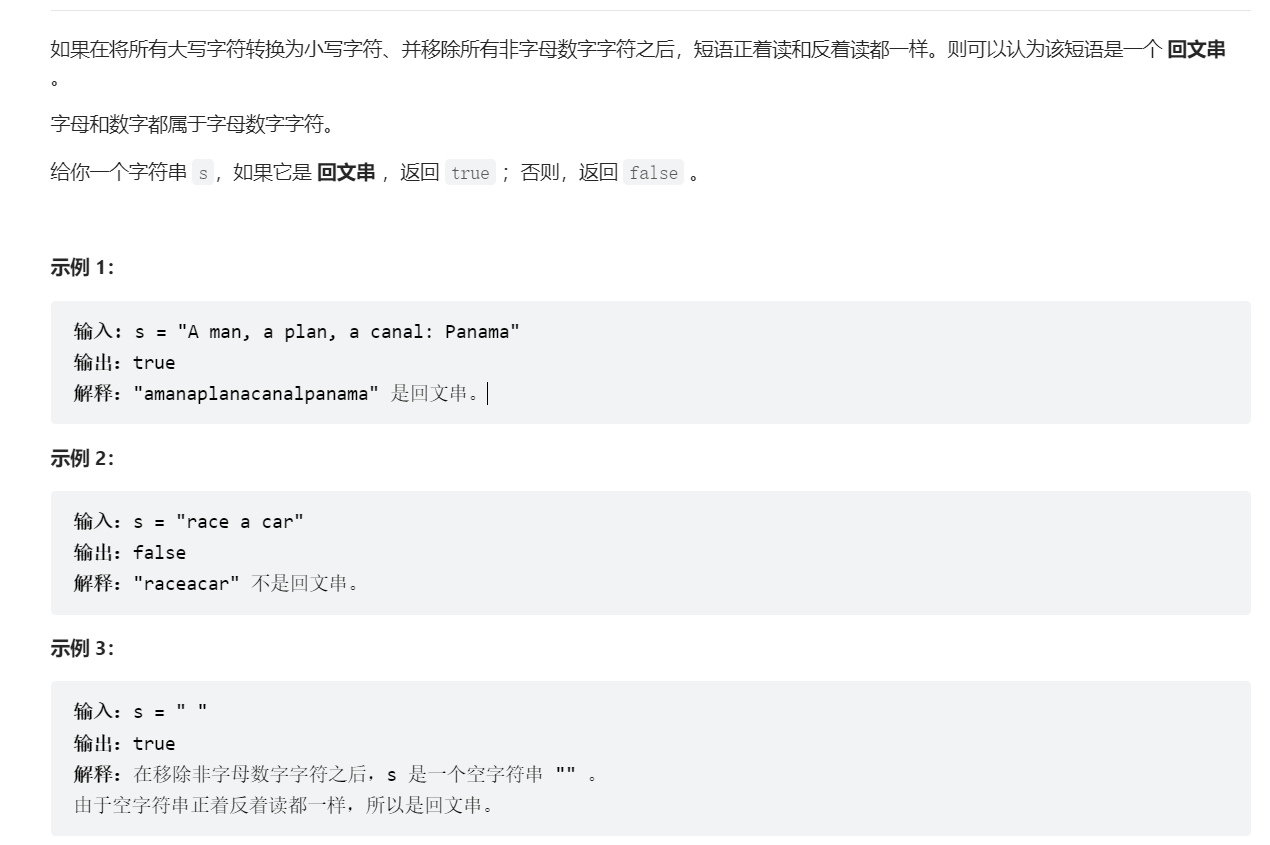
验证回文字符串

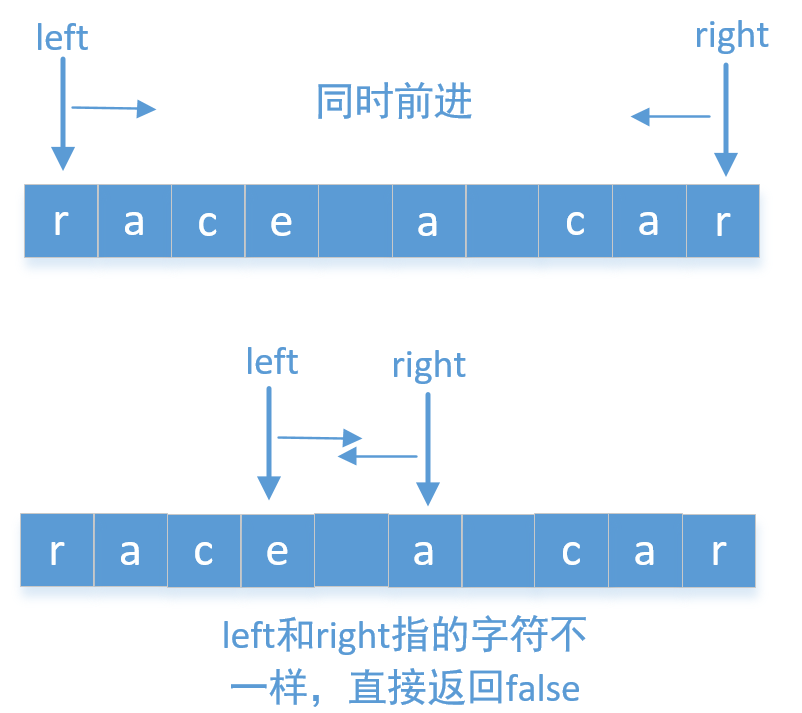
class Solution {
        public boolean isPalindrome(String s) {
        if (s.length() == 0)
            return true;
        int left = 0, right = s.length() - 1;
        while (left < right) {
            //因为题中说了，只考虑字母和数字，所以不是字母和数字的先过滤掉
            while (left < right && !Character.isLetterOrDigit(s.charAt(left)))
                left++;
            while (left < right && !Character.isLetterOrDigit(s.charAt(right)))
                right--;
            //然后把两个字符变为小写，在判断是否一样，如果不一样，直接返回false
            if (Character.toLowerCase(s.charAt(left)) != Character.toLowerCase(s.charAt(right)))
                return false;
            left++;
            right--;
        }
        return true;
    }
}

双指针的另一种写法：

public boolean isPalindrome(String s) {
    if (s == null || s.length() == 0)
        return true;
    s = s.toLowerCase();
    for (int i = 0, j = s.length() - 1; i < j; i++, j--) {
        while (i < j && !Character.isLetterOrDigit(s.charAt(i)))
            i++;
        while (i < j && !Character.isLetterOrDigit(s.charAt(j)))
            j--;
        if (s.charAt(i) != s.charAt(j))
            return false;
    }
    return true;
}

使用正则匹配：

public boolean isPalindrome(String s) {
    String actual = s.replaceAll("[^A-Za-z0-9]", "").toLowerCase();
    String rev = new StringBuffer(actual).reverse().toString();
    return actual.equals(rev);
}

递归方式实现：

public boolean isPalindrome(String s) {
    return isPalindromeHelper(s, 0, s.length() - 1);
}

public boolean isPalindromeHelper(String s, int left, int right) {
    if (left >= right)
        return true;
    while (left < right && !Character.isLetterOrDigit(s.charAt(left)))
        left++;
    while (left < right && !Character.isLetterOrDigit(s.charAt(right)))
        right--;
    return Character.toLowerCase(s.charAt(left)) == Character.toLowerCase(s.charAt(right)) && isPalindromeHelper(s, ++left, --right);
}

字符串转换整数 (atoi)

class Solution {
    public int myAtoi(String s) {
            char[] chars = s.toCharArray();
            int length = chars.length;
            int index = 0;
            // 先去除空格
            while (index < length && chars[index] == ' '){
                index++;
            }
            // 极端情况 "  " 和""
            if(index >= length){
                return 0;
            }
            // 再判断符号
            int sign =  1;
            if(chars[index] == '-' || chars[index] == '+'){
                if(chars[index] == '-'){
                    sign = -1;
                }
                index++;
            }
            int result = 0;
            int temp = 0;
            while (index < length){
                int num = chars[index] - '0';
                if(num > 9 || num < 0){
                    break;
                }
                temp = result;
                result = result * 10 + num;
                // 越界后，数值和期望数值发生变化，取余再除10获取原始值，比对判断
                if(result/10 !=temp){
                    if(sign > 0){
                        return Integer.MAX_VALUE;
                    }else {
                        return Integer.MIN_VALUE;
                    }
                }
                index++;
            }
            return result*sign;
    }
}

实现 strStr()

暴力匹配：

class Solution {
    public int strStr(String haystack, String needle) {
        char[] hay = haystack.toCharArray();
        char[] nee = needle.toCharArray();
        for (int i = 0; i <= hay.length - nee.length; i++) {
            boolean found = true;
            for (int j = 0; j < nee.length; j++) {
                if (hay[i+j] != nee[j]) {
                    found = false;
                    break;
                }
            }
            if (found) {
                return i;
            }
        }
        return -1;
    }
}

一行代码搞定：

 public int strStr(String haystack, String needle) {
        return haystack.indexOf(needle);
    }
}

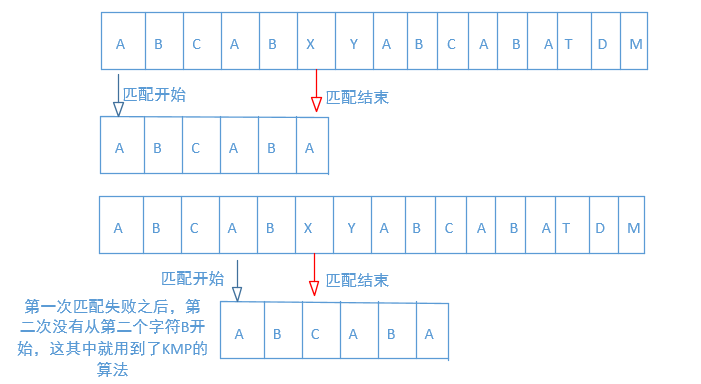
KMP算法：

public int strStr(String haystack, String needle) {
    if (needle.length() == 0)
        return 0;
    int i = 0;
    int j = 0;
    /**
     * 数组next表示pattern指定的下标前具有相同的字符串数量，语言组织能力不好，可能不是太好理解，我举个例子吧
     * ，比如ABCABA，数组next[0]是-1，这个是固定的，因为第一个A前面是没有字符的，next[1]是0，因为B的前面就一个A，没有
     * 重复的，所以是0,同理next[2]也是,next[3]也是0,而next[4]是1，因为next[4]所指向的是第二个B，第二个B前面有一个A和
     * 第一个A相同，所以是1,next[5]是2，因为next[5]所指向的是最后一个Ａ，因为前面的Ａ对比成功，并且Ｂ也对比成功，所以是２，
     * 也就是ＡＢ两个字符串匹配成功,再举个例子，比如WABCABA，数组除了第一个为-1，其他的都是为0，因为只有第一个匹配成功之后
     * 才能匹配后面的，虽然后面的AB和前面的AB匹配成功，但是后面AB的前面是C和前面AB的前面一个W不匹配，所以后面的匹配都是0.
     * 要记住只有指定字符前面的字符和第一个字符匹配成功的时候才能往后匹配，否则后面的永远都是先和第一个匹配。
     */
    int[] next = new int[needle.length()];
    getNext(needle, next);
    while (i < haystack.length() && j < needle.length()) {
        /**
         * 这里j等于-1的时候也只有在下面next数组赋值的时候才会出现，并且只有在数组next[0]的时候才会等于-1，
         其他时候是没有的，这一点要谨记，待会下面求next数组的时候就会用到。这里可以这样来理解，如果j不等于-1，
         并且下标i和j所指向的字符相等，那么i和j分别往后移一位继续比较，这个很好理解，那么如果j==-1的时候，就表示
         就表示前面没有匹配成功的，同时i往后移一位，j置为0（j==-1的时候，j++为0），再从0开始比较。
         */
        if (j == -1 || haystack.charAt(i) == needle.charAt(j)) {
            i++;
            j++;
        } else {
            /**
             * i = i - j + 1;
             j = 0;
             返回到指定的位置，不是返回到匹配失败的下一个位置，这里都好理解，重点是求数组next。
             这里只要j等于0，在next[j]赋值的之后，j就会等于-1；因为next[0]等于-1
             */
            j = next[j]; // j回到指定位置
        }
        if (j == needle.length())
            return i - j;
    }
    return -1;
}

private void getNext(String p, int next[]) {
    int len = p.length();
    int i = 0;
    int j = -1;
    next[0] = -1;//这个默认的，
    /**
     * 匹配的时候是当前字符的前一个和前面的匹配，所以最后一个是不参与匹配的，可以看strStr方法的注释，
     */
    while (i < len - 1) {
        if (j == -1 || p.charAt(i) == p.charAt(j)) {
            /**
             * 如果j不等于-1，指定的字符相等，那么i和j要往后移一位，这点很好理解，如果j为-1的时候，i往后移移位，j置为0
             * 重新开始匹配。next[i]是匹配成功的数量
             */
            i++;
            j++;
            next[i] = j;
        } else
        /**
         * 关键是这里不好理解，为什么匹配失败要让next[j]等于j，要记住这里的next[j]是指匹配成功的数量，有可能为0，也有可能是其他数.比如
         * 字符串ABCABXYABCABATDM,对应的next数组为{-1	0	0	0	1	2	0	0	1	2	3	4	5	1	0	0	}
         */
            j = next[j];
    }
}

x的n次幂

public class Solution {
    /**
     * @param x: the base number
     * @param n: the power number
     * @return: the result
     */
    public double myPow(double x, int n) {
        if (n == 0) {
            return 1;
        }
        long N = n;
        if (N < 0) {
            N = -N;
            x = 1 / x;
        }
        double ans = 1;
        while (N > 0) {
            if ((N & 1) == 1) {
                ans *= x;
            }
            x *= x;
            N >>= 1;
        }
        return ans;
    }
}

每次循环中都会判断当前指数 N 是否为奇数，如果是奇数，则将结果乘上 x，否则只是将 x 自乘，然后将指数 N 右移一位。这样就可以通过不断将指数除以 2，来逐步计算 x 的指数幂，优化计算效率。

旋转数字

我们称一个数 X 为好数, 如果它的每位数字逐个地被旋转 180 度后，我们仍可以得到一个有效的，且和 X 不同的数。要求每位数字都要被旋转。

如果一个数的每位数字被旋转以后仍然还是一个数字， 则这个数是有效的。0, 1, 和 8 被旋转后仍然是它们自己；2 和 5 可以互相旋转成对方（在这种情况下，它们以不同的方向旋转，换句话说，2 和 5 互为镜像）；6 和 9 同理，除了这些以外其他的数字旋转以后都不再是有效的数字。

现在我们有一个正整数 N, 计算从 1 到 N 中有多少个数 X 是好数？

class Solution {
    public int rotatedDigits(int n) {
        int count = 0;
        for(int i = 2; i <= n;i++){
            String s= String.valueOf(i);
            s = s.replaceAll("[+0, +1, +8]", "");
            if(!"".equals(s)){
                s = s.replaceAll("[+2,+5,+6+,9]","");
                if("".equals(s)){
                    count++;
                }
            }
        }
        return count;
    }
}

找到所有好下标

class Solution {
    public List<Integer> goodIndices(int[] nums, int k) {
        int n = nums.length;
        List<Integer> res = new ArrayList<>();
        int count = 1;
        if(k == 1){
            for(int i = 1;i < n - 1;i++){
                res.add(i);
            }
            return res;
        }
        for(int i = 1;i < n - k - 1;i++){
            if(nums[i] <= nums[i - 1] && nums[i + k + 1] >= nums[i + k]){
                count++;
                if(count >= k) {
                    res.add(i + 1);
                }
            }else{
                count = 1;
            }
        }
        return res;
    }
}

最长公共前缀

class Solution {
    public String longestCommonPrefix(String[] strs) {
        int m = strs.length;
        if(m == 0) return "";
        String ans = strs[0];
        for(int i = 1;i < m;i++){
            int j = 0;
            for(;j < ans.length() && j < strs[i].length();j++){
                if(ans.charAt(j) != strs[i].charAt(j)){
                    break;
                }
            }
            ans = ans.substring(0, j);
            if(ans.equals("")) return ans;
        }
        return ans;
    }
}

将数组和减半的最少操作次数

给你一个正整数数组 nums 。每一次操作中，你可以从 nums 中选择 任意 一个数并将它减小到 恰好 一半。（注意，在后续操作中你可以对减半过的数继续执行操作）

请你返回将 nums 数组和 至少 减少一半的 最少 操作数。

示例：

输入：nums = [5,19,8,1]
输出：3
解释：初始 nums 的和为 5 + 19 + 8 + 1 = 33 。
以下是将数组和减少至少一半的一种方法：
选择数字 19 并减小为 9.5 。
选择数字 9.5 并减小为 4.75 。
选择数字 8 并减小为 4 。
最终数组为 [5, 4.75, 4, 1] ，和为 5 + 4.75 + 4 + 1 = 14.75 。
nums 的和减小了 33 - 14.75 = 18.25 ，减小的部分超过了初始数组和的一半，18.25 >= 33/2 = 16.5 。
我们需要 3 个操作实现题目要求，所以返回 3 。
可以证明，无法通过少于 3 个操作使数组和减少至少一半。

public class Solution {
    public int halveArray(int[] nums) {
        PriorityQueue<Double> pq = new PriorityQueue<Double>((a, b) -> b.compareTo(a));
        for(int num : nums){
            pq.offer((double) num);
        }
        int res = 0;
        double sum = 0;
        for(int num : nums) {
            sum += num;
        }
        double sum2 = 0.0;
        while(sum2 < sum / 2){
            double x = pq.poll();
            sum2 += x / 2;
            pq.offer(x / 2);
            res++;
        }
        return res;
    }
}

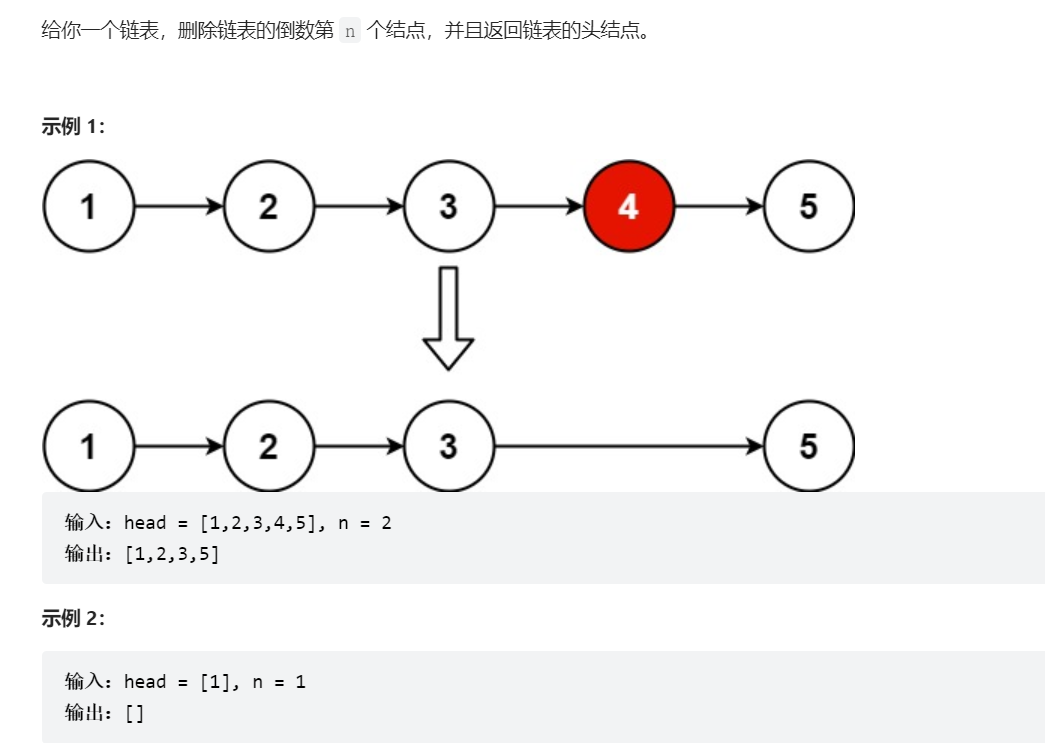
链表

删除链表的倒数第N个节点

提示：

• 链表中结点的数目为 sz
• 1 <= sz <= 30
• 0 <= Node.val <= 100
• 1 <= n <= sz

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummy = new ListNode(0);
        dummy.next = head;

        ListNode fast = dummy;
        for(int i = 0;i < n;i++){
            fast = fast.next;
        }
        ListNode slow = dummy;
        while(fast.next != null){
            fast = fast.next;
            slow = slow.next;
        }

        slow.next = slow.next.next;
        return dummy.next;
    }
}

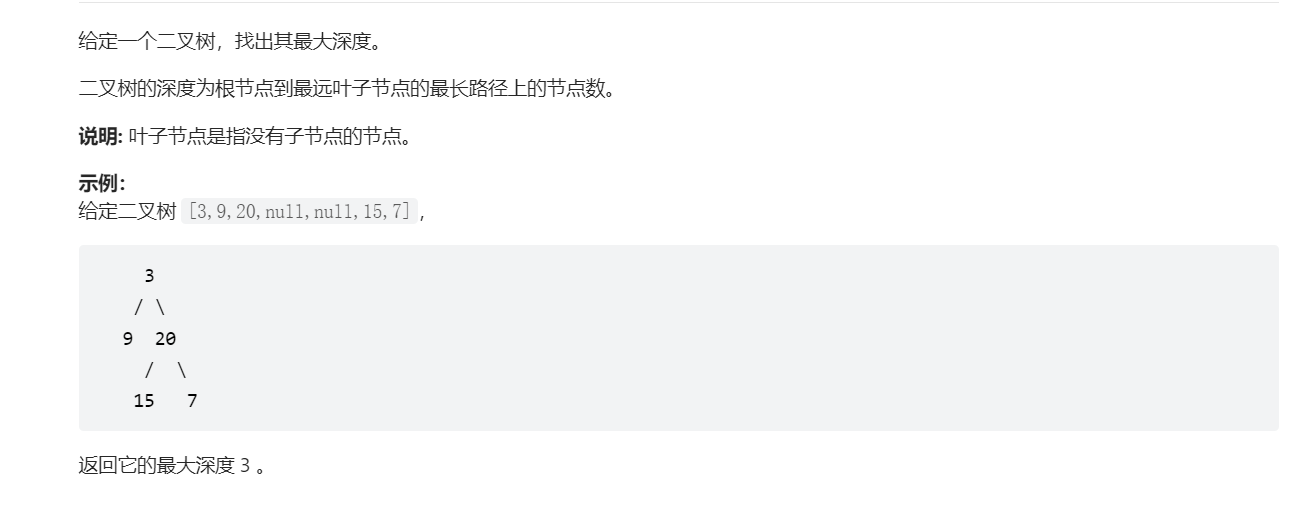
树

二叉树的最大深度

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null) return 0;
        else{
            return Math.max(maxDepth(root.left)+1, maxDepth(root.right)+1);
        }
    }
}

验证二叉搜索树

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isValidBST(TreeNode root) {
        return isValidBST(root, null, null);
    }

    public boolean isValidBST(TreeNode root, Integer min, Integer max) {
        if(root == null) return true;
        if(min != null && root.val <= min) return false;
        if(max != null && root.val >= max) return false;
        return isValidBST(root.left, min, root.val) && isValidBST(root.right, root.val, max);
    }
}